Vật lý 12- Sự giao thoa của sóng
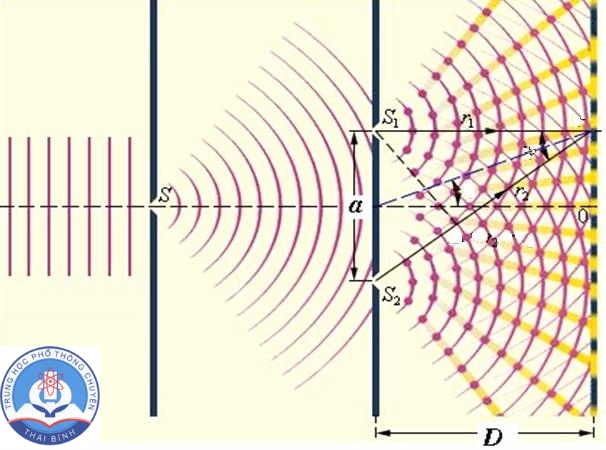
1. Khái niệm về nguồn kết hợp, sóng kết hợp
a. Nguồn kết hợp:
- Hai nguồn A, B được gọi là nguồn kết hợp nếu chúng có cùng tần số và độ lệch pha không đổi (hay cùng pha).
b. Sóng kết hợp:
- Hai sóng kết hợp là hai sóng được phát ra từ các nguồn kết hợp.
2. Khái niệm giao thoa sóng
Giao thoa sóng là sự tổng hợp của hai hay nhiều sóng kết hợp mà cho trên phương truyền sóng những điểm dao động với biên độ cực đại hoặc những điểm dao động với biên độ cực tiểu (những điểm dao động với biên độ bằng 0 hoặc không dao động).
* Chú ý:
Ngoài khái niệm như trên thì ta còn có thể nói sự giao thoa sóng chính là sự tổng hợp của hai dao động điều hòa.
3. Lý thuyết giao thoa
Giả sử có hai nguồn sóng kết hợp đặt tại hai điểm A và B dao động với cùng biên độ, cùng tần số với phương trình tương ứng là:;
.
Xét một điểm M cách các nguồn A, B các khoảng cách tương ứng là d1 và d2 như hình vẽ.
Phương trình sóng tại M do sóng từ nguồn A truyền đến là:
Phương trình sóng tại M do sóng từ nguồn B truyền đến là:
Do sóng truyền từ các nguồn là sóng kết hợp nên tại M có sự giao thoa của hai sóng phát ra từ hai nguồn.
Khi đó phương trình dao động tổng hợp tại M là:
Vậy phương trình dao động tổng hợp tại M là:
Ta xét một số trường hợp thường gặp:
Trường hợp 1:
, (Hai nguồn dao động cùng pha)
Khi đó phương trình dao động của hai nguồn là:
Phương trình sóng tại M do sóng từ nguồn A truyền đến là:
Phương trình sóng tại M do sóng từ nguồn B truyền đến là:
Phương trình dao động tổng hợp tại M là:
Vậy phương trình dao động tổng hợp tại M là:
* Nhận xét:
- Pha ban đầu của dao động tổng hợp là:
- Biên độ dao động tổng hợp tại M là:
• Biên độ dao động tổng hợp cực đại khi:
Vậy khi hiệu đường truyền bằng một số nguyên lần bước sóng thì dao động tổng hợp có biên độ cực đại,
• Biên độ dao động tổng hợp cực tiểu (bị triệt tiêu) khi:
Vậy khi hiệu đường truyền bằng một số nguyên lẻ lần nửa bước sóng thì dao động tổng hợp có biên độ bị triệt tiêu,
Trường hợp 2:
, (Hai nguồn dao động ngược pha)
Khi đó phương trình dao động của hai nguồn là:
Phương trình sóng tại M do sóng từ nguồn A truyền đến là:
Phương trình sóng tại M do sóng từ nguồn B truyền đến là:
Phương trình dao động tổng hợp tại M là:
Vậy phương trình dao động tổng hợp tại M là
* Nhận xét:
- Pha ban đầu của dao động tổng hợp là:
- Biên độ dao động tổng hợp tại M là:
• Biên độ dao động tổng hợp cực đại khi:
Vậy khi hiệu đường truyền bằng một số nguyên lẻ lần nửa bước sóng thì dao động tổng hợp có biên độ cực đại, AM.max = 2A
• Biên độ dao động tổng hợp cực tiểu (bị triệt tiêu) khi:
Vậy khi hiệu đường truyền bằng một số nguyên lần bước sóng thì dao động tổng hợp có biên độ bị triệt tiêu, AM.min = 0
Trường hợp 3:
, (Hai nguồn dao động ngược pha)
Khi đó phương trình dao động của hai nguồn là:
Phương trình sóng tại M do sóng từ nguồn A truyền đến là:
Phương trình sóng tại M do sóng từ nguồn B truyền đến là:
Phương trình dao động tổng hợp tại M là:
Vậy phương trình dao động tổng hợp tại M là:
* Nhận xét:
- Pha ban đầu của dao động tổng hợp là:
- Biên độ dao động tổng hợp tại M là:
• Biên độ dao động tổng hợp cực đại khi:
Vậy khi hiệu đường truyền bằng một số nguyên lẻ lần nửa bước sóng thì dao động tổng hợp có biên độ cực đại, AM.max = 2A
• Biên độ dao động tổng hợp cực tiểu (bị triệt tiêu) khi:
Vậy khi hiệu đường truyền bằng một số nguyên lần bước sóng thì dao động tổng hợp có biên độ bị triệt tiêu, AM.min = 0
* KẾT LUẬN:
• Nếu hai nguồn cùng pha thì điều kiện để dao động tổng hợp có biên độ cực đại là d2 - d1 = kλ, biên độ triệt tiêu khi:
• Nếu hai nguồn ngược pha thì điều kiện để dao động tổng hợp có biên độ cực đại là d2 - d1 = kλ, biên độ triệt tiêu khi:
• Quỹ tích các điểm dao động với biên độ cực đại hay cực tiểu là đường cong Hypebol nhận A, B làm các tiêu điểm. Các đường Hypebol được gọi chung là vân giao thoa cực đại hoặc cực tiểu.
Khi d2 - d1 = kλ, k = 0 là đường trung trực của AB, k = ±1; k = ± 2…là các vân cực đại bậc 1, bậc 2…
Khi, k = 0 và k = –1 là các vân bậc 1, k = 1 và k = –2 là các vân bậc 1...
(Hình vẽ minh họa)

4. Ứng dụng của giao thoa sóng
a. Ứng dụng 1:
- Xác định đối tượng đang xét có bản chất sóng hay không
b. Ứng dụng 2: (Tìm số điểm dao động với biên độ cực đại, cực tiểu trên đoạn AB)
* Trường hợp 1: Hai nguồn dao động cùng pha
• Tìm số điểm dao động với biên độ cực đại trên AB
Giả sử M là một điểm dao động với biên độ cực đại trên AB, do hai nguồn dao động cùng pha nên có d2 - d1 = kλ. Mặt khác lại có d2 + d1 = AB
Từ đó ta có hệ phương trình:
Do M nằm trên đoạn AB nên có:
Số các giá trị k nguyên thỏa mãn hệ thức trên chính là số điểm dao động với biên độ cực đại cần tìm. Với những giá trị k tìm được thì hệ thứccho phép xác định vị trí các điểm M trên AB.
• Tìm số điểm dao động với biên độ cực tiểu trên AB
Giả sử M là một điểm dao động với biên độ cực tiểu trên AB, do hai nguồn dao động cùng pha nên
.
Mặt khác lại có:d2 + d1 = AB
Từ đó ta có hệ phương trình:
Do M nằm trên đoạn AB nên có:
Số các giá trị k nguyên thỏa mãn hệ thức trên chính là số điểm dao động với biên độ cực tiểu cần tìm. Với những giá trị k tìm được thì hệ thức (**) cho phép xác định vị trí các điểm M trên AB.
* Trường hợp 2: Hai nguồn dao động ngược pha
• Tìm số điểm dao động với biên độ cực đại trên AB
Giả sử M là một điểm dao động với biên độ cực đại trên AB, do hai nguồn ngược pha nên ta có:
.
Mặt khác lại có: d2 + d1 = AB.
Từ đó ta có hệ phương trình:
Do M nằm trên đoạn AB nên có
Số các giá trị k nguyên thỏa mãn hệ thức trên chính là số điểm dao động với biên độ cực đại cần tìm. Với những giá trị k tìm được thì hệ thức (**) cho phép xác định vị trí các điểm M trên AB.
• Tìm số điểm dao động với biên độ cực tiểu trên AB
Giả sử M là một điểm dao động với biên độ cực tiểu trên AB, do hai nguồn dao động ngược pha nên có d2 - d1 = kλ. Mặt khác lại có: d2 + d1 = AB.
Từ đó ta có hệ phương trình:
Do M nằm trên đoạn AB nên có:
Số các giá trị k nguyên thỏa mãn hệ thức trên chính là số điểm dao động với biên độ cực tiểu cần tìm. Với những giá trị k tìm được thì hệ thứccho phép xác định vị trí các điểm M trên AB.
* Chú ý:
Từ hệ thứcta tính được khoảng cách giữa hai vân giao thoa cực đại gần nhau nhất (cũng chính là vị trí của hai điểm M gần nhau nhất dao động với biên độ cực đại) là:
Tương tự khoảng cách giữa hai vân cực tiểu gần nhau nhất cũng là. Khoảng cách giữa một vân cực đại và một vân cực tiểu gần nhau nhất là

5. Các ví dụ điển hình
Ví dụ 1: Trên mặt thoáng của chất lỏng có hai nguồn kết hợp A, B có phương trình dao động là:
. Tốc độ truyền sóng là v = 3m/s.
a. Viết phương trình sóng tại M cách A, B một khoảng lần lượt d1 = 15cm; d2 = 20cm.
b. Tính biên độ và pha ban đầu của sóng tại N cách A và B lần lượt 45cm và 60cm.
* Hướng dẫn giải:
a. Bước sóng:
Ta có:
Phương trình dao động tổng hợp tại M là:
=
Thay các giá trị của d1, d2 và λ vào ta được:
b. Áp dụng công thức tính biên độ và pha ban đầu ta được:
Pha ban đầu tại N là:
Ví dụ 2: Trong giao thoa sóng nước, hai nguồn kết hợp A, B cách nhau 10(cm) dao động với phương trình lần lượt là:,
. Tốc độ truyền sóng là v = 0,5 (m/s).
a. Viết phương trình dao động tổng hợp tại điểm M cách các nguồn A, B lần lượt d1, d2
b. Tìm số điểm dao động với biên độ cực đại trên đoạn AB.
c. Tìm số điểm dao động với biên độ cực tiểu trên AB.
* Hướng dẫn giải:
a. Phương trình sóng tại M do sóng từ nguồn A truyền đến là:
Phương trình sóng tại M do sóng từ nguồn B truyền đến là:
Phương trình dao động tổng hợp tại M là:
Vậy phương trình dao động tổng hợp tại M là:
b. Từ câu a, ta tìm được biên độ dao động tổng hợp tại M là:
Biên độ dao động tổng hợp cực đại khi:
Mặt khác M lại thuộc đoạn AB nên có d2 + d1 = AB, từ đó ta được hệ phương trình:
Do M nằm trên đoạn AB nên có:
Thay số AB = 10 cm,ta được:
Vậy có 10 điểm dao động với biên độ cực đại trên AB.
c. Tương tự câu b, ta giải hệ tìm điều kiện cực tiểu khi hai nguồn ngược pha:
Do M nằm trên đoạn AB nên có:
Vậy có 11 điểm dao động với biên độ cực tiểu trên đoạn AB.
Ví dụ 3: Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A, B dao động với tần số f =15Hz và cùng pha. Tại một điểm M cách A, B những khoảng d1=16cm, d2=20cm sóng có biên độ cực tiểu. Giữa M và đường trung trực của AB có hai dãy cực đại. Tốc truyền sóng trên mặt nước là bao nhiêu?
* Hướng dẫn giải:
Hai nguồn dao động cùng pha nên điều kiện để M dao động với biên độ cực tiểu là:
Do giữa M và đường trung trực của AB có hai dãy cực đại khác nên tại M là đường cực tiểu thứ 3 ở bên phải đường trung trực của AB. Đường này ứng với giá trị k = 2. Thay vào biểu thức trên ta được:.
Khi đó tốc độ truyền sóng là v = λ.f = 1,6.15 = 24 (cm/s).
Ví dụ 4: Hai nguồn kết hợp A, B cách nhau 50 (mm) dao động với cùng phương trình:
. Xét về cùng một phía với đường trung trực của AB ta thấy vân giao thoa bậc k đi qua điểm M thỏa mãn MA - MB = 12 (mm) và vân giao thoa bậc (k + 3) cùng loại với vân giao thoa bậc k, (tức là cùng là vân cực đại hoặc cùng là vân cực tiểu) đi qua điểm M’ có M’A – M’B = 36 (mm).
a. Tính giá trị của λ, v.
b. Điểm gần nhất dao động cùng pha với hai nguồn nằm trên đường trung trực của AB cách A bao nhiêu?
* Hướng dẫn giải:
a. Ta xét hai trường hợp
Trường hợp 1: M và M’ cùng là các điểm dao động với biên độ cực đại. Do hai nguồn cùng pha nên ta có:
,(loại)
Trường hợp 2: M và M’ cùng là các điểm dao động với biên độ cực tiểu. Do hai nguồn cùng pha nên ta có:
Thay k = 1 vào ta tìm được λ = 12(mm) => v = λ.f = 12.100 = 1200(mm/s) = 1,2(m/s).
b. Gọi N là một điểm nằm trên đường trung trực của AB, d2 = d1
Khi đó pha ban đầu của N là:
Độ lệch pha của N với hai nguồn là:
Để điểm N dao động cùng pha với hai nguồn thì:
Vậy điểm N gần nhất mà dao động cùng pha với hai nguồn cách A và B một khoảng là 12(mm).
BÀI TẬP LUYỆN TẬP
Bài 1: Tại hai điểm O1, O2 cách nhau 48cm trên mặt chất lỏng có hai nguồn phát sóng dao động theo phương thẳng đứng với phương trình: u1 = 5sin100πt(mm) và u2 = 5sin(100πt + π)(mm). Vận tốc truyền sóng trên mặt chất lỏng là 2m/s. Coi biên độ sóng không đổi trong quá trình truyền sóng.
a. Viết phương trình dao động tổng hợp tại điểm M cách các nguồn lần lượt là d1 và d2
b. Trên đoạn O1O2 có số cực đại giao thoa là bao nhiêu?
Đáp án : b. Có 24 điểm dao động với biên độ cực đại.
Bài 2: Hai nguồn kết hợp A, B cách nhau 10cm dao động cùng pha cùng tần số 20Hz. Vận tốc truyền sóng trên mặt chất lỏng là 1,5m/s.
a) Tính số điểm không dao động trên đoạn AB
b) Tính số đường không doa động trên mặt chất lỏng.
Đáp số : a) Số điểm không dao động là 14.
b) Số đường không dao động là 14 đường.
Để thắc mắc và góp ý về bài này, vui lòng ấn vào đây
Tác giả bài viết: Hoàng Giang sưu tầm
Từ khóa: giao thoa sóng
Tin xem nhiều
Thống kê truy cập
- Đang truy cập17
- Hôm nay7,945
- Tháng hiện tại31,962
- Tổng lượt truy cập38,142,864
































































